Divisibility Rules Upto 15: Definition, Examples & Explained

Here are some quick tricks you can learn to see if a number is divisible (can be divided by) another number. How!

OK … You can see that 27 is divisible by 3, meaning 3 goes to 27.

But, can you quickly tell if 3 goes into 537? Without doing long division? I can! And not just because I’m a super math brilliant, I know some math tricks. These are ways to learn because they will save you time!

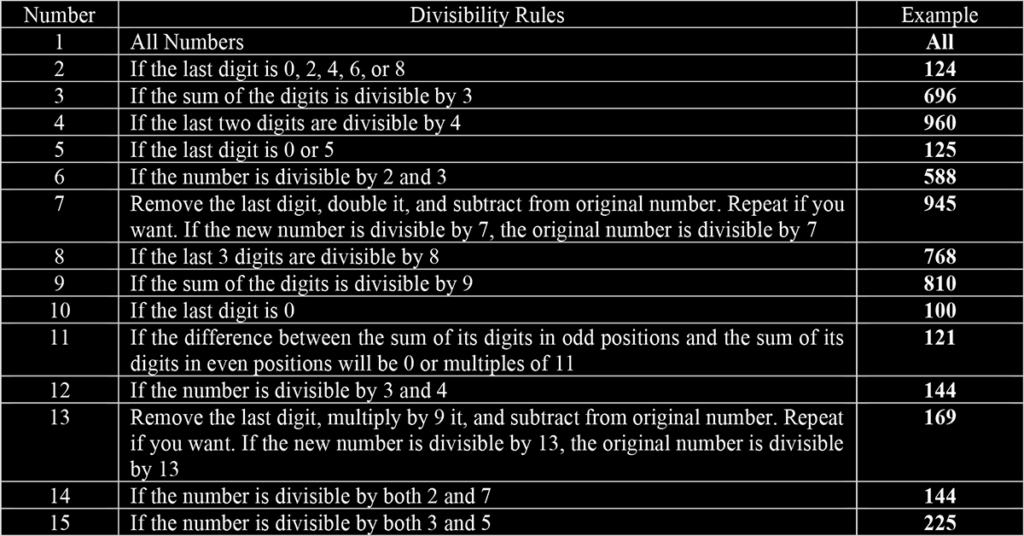
Divisibility Rule of 1:

Every number is divisible by 1.

Divisibility rules for 2:

A number is divisible by 2 if it is even.

Here’s another way to define this one:

A number is divisible by 2 if its last digit is 0, 2, 4, 6, or 8

Let’s try an easy example.

Does 2 go into 20?

(Is 20 divisible by 2?)

Yes, since the last digit is 6 (it’s even).

Here harder example:

Is 290986 divisible by 2?

Yes, since the last digit is 6 (it’s even)

What about this one?

Is 2719 divisible by 2?

No, since the last digit is 9 and it’s not an even number.

The next divisibility test trick is harder, but once you get good at, it, you can do it easily! 

Divisibility rules for 3:

A number is divisible by 3 if the sum of its digits is divisible by 3.

Why?

Don’t worry … this is easy!

Let’s do one:

Does 3 go into 2610?

First step: Add all digits that’s mean 2 + 6 + 1 + 0 = 9

Second step: Check that 9 is divisible by 3. Yes!

So, 2610 is divisible by 3! (Check your result with a calculator or Do some long division)

Here’s another one:

Does 3 go into 80354?

8 + 0 + 3 + 5 + 4 = 20

3 does not go into 20,

So, 80354 is not divisible by 3!

Divisibility rule of 4:

This one works great – about half of the time.

A number is divisible by 4 if the last two digits are a number that is divided by 4.

Let me make that clear: Look at the following number

78948

Is 48 divisible by 4? Yes!

So the number is divisible by 4.

Try it another:

Is 123 divisible by 4? Nope!

The last two digits 23 are not divisible by 4.

Divisibility rule of 5:

A number is divisible by 5 If the last digit is 0 or 5.

Let’s try an easy example.

Is 25 divisible by 5?

Yes, since the last digit is 5. We know that (25 ÷5=5)

Here one harder example:

Is 495380 divisible by 5?

Yes, since the last digit is 0.

What about this one?

Is 9826827 divisible by 5?

No, since the last digit is not a 0 or 5.

Divisibility rule of 6:

A number is divisible by 6 if it’s divided by 2 AND 3.

So, you have to do the divisibility test for 2 and the divisibility test for 3 … If they both satisfy, then you’re the right way to go!

Check out an example:

Is 36 divisible by 6?

The divisibility test of 2: 36 is even (the last digit is 2). So, 36 is divisible by 2….

Divisibility test of 3: 3 + 6 = 9 which is divisible by 3 … So, 36 is divisible by 6!

What about this one?

Does 6 go into 54863?

No, it is not even so 2 doesn’t go in.

Divisibility Rule for 7:

The divisibility rule of 7 is harder, but if you follow this step, you can do it easily! 

Step 1: Remove the last digit of a given number and double it.

Step 4: Subtract it from the remaining number.

Step 3: Is the number 0 or a known 2-digit multiple of 7? If it is then it is divided by 7.

Step 4: If it is not divisible by 7 then repeat this process and continue.

Let’s try an example:

Is 2037 divisible by 7?

We explain it.

First, remove 7 from the original number and double it, which becomes 7 × 2 = 14.

Now the remaining number is 203, so 203 – 14 = 189.

Repeat the process one more time, we have 9 × 2 = 18.

The remaining number is 18. So, 18 – 18 = 0.

Wow! 0 is divisible by 7, hence the number 2037 is divisible by 7.

Divisibility rules for 8:

This is similar to the test for 4, but even less useful.

A number is divisible by 8 if the last three digits are a number that’s divisible by 8.

Therefore we have to look at a three-digit number, we’re probably not going to be able to eyeball this one. We’ll probably need to do some long division or use a calculator.

Is 900200 divisible by 8?

Ok, we need to check to see if 8 goes into 200.

Long division Time! Or 200 ÷ 8 = 25.

So, 985200 is divisible by 8.

How about this one?

Is 98066 divisible by 8?

Hey, this one is easy! Is 66 is divisible by 8?

No way. So 98066 isn’t divisible by 8.

Divisibility rule of 9:

A number is divisible by 9 if the Sum of the digits is divisible by 9.

Let’s do one:

Is 7821 divisible by 9?

Step one: Add the digits 7 + 8 + 2 + 1 = 18

Step second: Is 18 divided by 9? Yes!

So, 7821 is divisible by 9! (Check your result with a calculator or

Do some long division)

Here’s another one:

Does 9 go into 80354?

8 + 0 + 3 + 5 + 4 = 20

9 does not go into 20,

Check out the answer for the “nines” multiplication tables!

9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108

Divisibility by 10:

There is the easiest one!

A number is divisible by 10 if the last digit is 0.

Is 50 divisible by 10?  Yes!

Is 899 divisible by 10? No!

Now that you’ve learned divisibility rules for numbers 2 to 10, let’s move on to 11 to 15. These rules are a little tricky at first, but with practice, you’ll master them!

Divisibility Rule for 11:

A number is divisible by 11 if the difference between the sum of its digits in odd positions and the sum of its digits in even positions will be 0 or multiples of 11.

Let’s check how it works.

Step 1: Calculate the sum of digits in the “odd” positions.

Step 2: Calculate the sum of digits in the “even” positions.

Step 3: Calculate the difference between two sums.

Step 4: Check if the result is 0 or multiples of 11.

OK, For clarity let’s try an example:

Is 25916 divisible by 11?

Step one: Odd-position digits: 2 + 9 + 6 = 17.

Step 2:  Even-position digits: 5 + 1 = 6.

Step 3: Difference: 17 – 6 = 11.

Step 4:  Wow! 11 is divisible by 11, the number 25916 is divisible by 11.

Another example:

Is 39465 divisible by 11?

Step 1: Odd-position digits: 3 + 4 + 5 = 12.

Step 2: Even-position digits: 9 + 6 = 15.

Step 3: Subtract: 12 – 15 = -3.

Step 4: Nope! -3 is not divisible by 11, the number 39465 is not divisible by 11.

Divisibility Rule for 12:

A number is divisible by 12 if it is divisible by both 3 and 4.

Now, time to remember the previous rules.

A number is divisible by 3 (the sum of digits divisible by 3).

A number is divisible by 4 (the last two digits are divisible by 4).

Let’s do an easy example:

Is 180 divisible by 12?

1. Divisibility test of 3: 1 + 8 + 0 = 9, and 9 is divisible by 3.

2. Divisibility test of 4: The last two digits are 80, and 40 ÷ 4 = 20, which is divisible by 4.

3. 180 satisfies both 3 and 4.

Therefore, 180 is divisible by 12.

Let’s do a hard one:

Is 9471 divisible by 12?

1. Divisibility test of 3: 9 + 4 + 7 + 1 = 21, and 21 is divisible by 3.

2. Divisibility test of 4: The last two digits are 71, 71 is not divisible by 4.

3. 9471 does not satisfy both 3 and 4.

Therefore, 9471 is divisible by 12

Divisibility Rule for 13:

This one is a bit tricky but can be mastered! A number is divisible by 13 if you can remove the last digit, multiply it by 9, and subtract that result from the remaining number (sometimes you may have to repeat this process). If the result is divisible by 13, then the original number is divisible by 13.

Let’s try an example:

Is 221 divisible by 13?

step 1: Remove the last digit: 1.

Step 2: Multiply by 9: 1 × 9 = 9.

Step 3: Subtract from the remaining number: 22 – 9 = 13.

Step 4: Since 13 ÷ 13 = 1.

Hence, 221 is divisible by 13.

Another example:

Is 3705 divisible by 13?

Step 1: Remove the last digit: 5.

Step 2: Multiply by 9: 5 × 9 = 45.

Step 3: Subtract from the remaining number: 370 – 45 = 325.

Step 4: Now repeat one more time i.e. 32 – 45 = -13.

Step 5:  -13 is divisible by 13.

Therefore,  3705 is divisible by 13.

Divisibility Rule for 14:

A number is divisible by 14 if it is divisible by both 2 and 7.

For Example:

Is 336 divisible by 14?

Divisibility check by 2: 336 is even, so 336 is divisible by 2.

Divisibility check by 7: Follow the rule of 7: Remove the last digit (6), double it (6 × 2 = 12), and subtract it from the remaining number (33 – 12 = 21). 21 is divisible by 7

So, 336 is divisible by 14.

Divisibility Rule for 15:

A number is divisible by 15 if it is divisible by both 3 and 5.

Let’s do an example:

Is 225 divisible by 15?

1. Divisibility test of 3: 2 + 2 + 5 = 9, and 9 is divisible by 3.

2. Divisibility test of 5: The last digit is 5, so the number is divisible by 5.

3. It satisfies both conditions.

Therefore 225 is divisible by 15.

Another example:

Is 1310 divisible by 15?

1. Check the divisibility of 3: 1 + 3 + 1 + 0 = 5, and 5 is does not divisible by 3.

2. Even though the number is divisible by 5 (the last digit is 0), it does not meet the condition for 3.

Therefore, 1310 is not divisible by 15.

Practice Divisibility Rules Question:

Is 719 divisible by 2?

Is 523 divisible by 3?

Is 9430 is divisible by 4?

Is 7250 divisible by 5?

Does 6 go into 9864?

Is 8048 is divisible by 8?

Is 55289 divisible by 9?

Is 789 divisible by 10?

Is 3495 divisible by 11?

Is 2844 divisible by 12?

Is 1403 divisible by 13?

Is 5074 divisible by 14?

Is 6310 divisible by 15?

FAQ About Divisibility Rules